马来文数学⁹(Bab6 Persamaan Linear 线性方程)

Question

请问这题怎样做？谁能教？求解鸭……꒦ິ^꒦ິ

Comments

这个是不是bab6的

---

是的

---

是要找x是吗

---

啊对

---

就是除了长方形以外的地方（三角形）的面积是22，然后长方形面积是46
长方形面积=8（x+2）
                     
多于的三角形=8（（2x+1）-（x+2））
                         =8（2x+1-x-2）

---

还有一个快一点的方法，要用梯形公式。

---

你会？

---

有哪里不明白吗？

---

哎呀 我看错了，题目要的是 (x+2)等于多少和（2x+1）等于多少

---

好，我改答案。

---

这个分类也得改。。。

Answer 1

方法1:（给 Bab 10 的）

梯形公式：

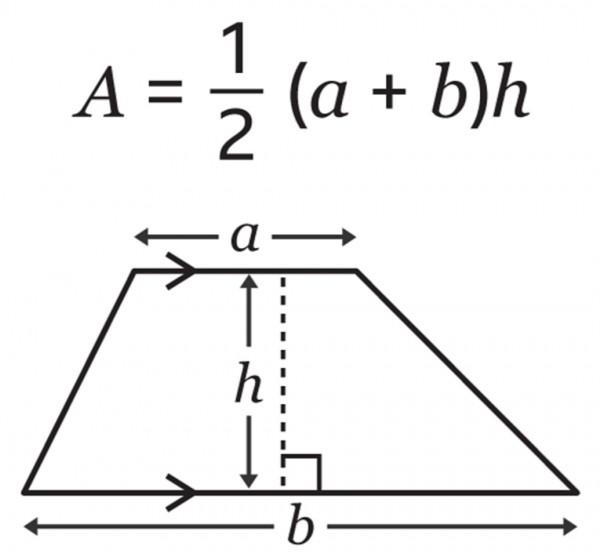
其中 a 和 b 分别是 上底和下底 ，也就是 这个 梯形 的base。

而 h 是梯形的高。

---

回到问题，a 是 x+2, 

b 是 2x+1, 

而 h 是 8cm

根据 梯形面积公式列方程

1/2（x+2+2x+1) ✖️ 8 =68

（3x+3) ✖️8=68✖️2

24x +24=136

24x=136-24

24x=112

 所以，x=(14/3) cm

or (老师可能 prefer） x=(4 2/3) cm

---

你说要找上底和下底 的长度：

x+2
= (4 2/3) + 2
= 6 2/3 cm

2x+1
= 2(14/3) + 1
= 28/3 + 1
= 31/3
= 10 1/3 cm

如果你要找 “上底“和“下底”的和，那答案是 3x+3= 6 2/3 + 10 1/3=17cm

---

方法2: （给 Bab 6 的）

假如你没学过梯形面积公式，也可以这样做：（比较慢，但也可以解出这答题）

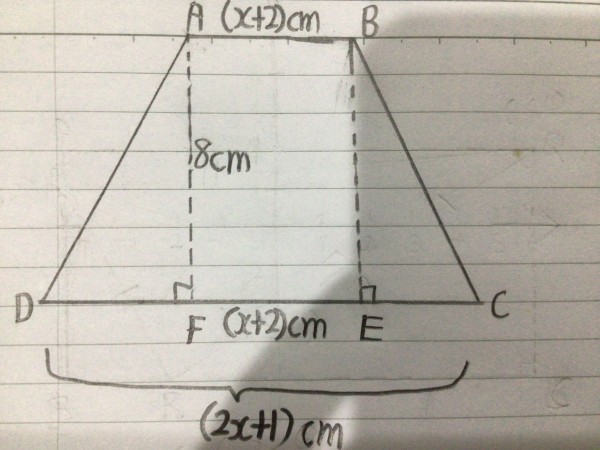
首先, AB=FE=x+2 因为 ABEF 是长方形，

Area of rectangle ABEF =8(x+2)。

DF+EC= DC- FE= （2x+1)-(x+2)=x-1

首先，Area of triangle ADF= 1/2 ✖️ DF ✖️8

Area of triangle BEC= 1/2 ✖️EC ✖️8

Area of triangle ADF+ Area of triangle BEC

=1/2 ✖️DF ✖️8  +  1/2 ✖️ EC ✖️8

*=1/2 ✖️ （DF+EC）✖️8 【这里有用到 Distributive Law，Form 1 第一课学的】

=1/2 ✖️（x-1) ✖️8

列方程：

Area of rectangle ABEF + Area of triangle ADF+ Area of triangle BEC =Area of trapezium

8(x+2) + 1/2 ✖️（x-1) ✖️8=68

8x+16+4(x-1)=68

8x+16+4x-4=68

12x             =68-16+4

12x             =56

x                =56/12

所以，x= 4 2/3 cm

---

你要找上底和下底 的长度:

x+2 = (4 2/3) + 2 = 6 2/3 cm

2x+1 = 2(14/3) + 1 = 28/3 + 1 = 31/3 = 10 1/3 cm

如果你要找上底和下底的和，那答案是 

3x+3= 6 2/3 + 10 1/3=17cm

Comments

可是老师给的答案是 3x + 3 = 17

---

因为你有的formula是Bab10的，我这一题是Bab6的

---

请看 方法2  谢谢。

---

你的答案是 找 上底+下底 的和，就是将 6 2/3+10 1/3 的和加起来。

你之前的评论 讲 “ 题目要的是 (x+2)等于多少和（2x+1）等于多少”

我还以为你是问 这两条边 分别为多少，所以明白错了。

---

我改了答案，请采纳回答。

Answer 2

（2x+1）-（x+2）

=左和右加起来的长度

=2x+1-x-2

=2x-x+1-2

=x+（-1）

OK先算三角形的面积

8（x+（-1））

__________________

2

   8x-8

=  -------

       2

ok 所以他们面积就是

（8x-8）

-------------+8(x+2)=68

      2

8x-8

------------+(8x+16)=68

      2

8x-8

-------- +8x+16=68

 2       

8x-8 +16x +32=136

8x+16x-8+32=136

24x-8+32=136

24x+24=136

24x=136-24

24x=112

X=¹¹²/24

x=¹⁴/3

---

算那两个ungkapan

x+2

=¹⁴/3+2

=²⁰/3

=6⅔

2x+1

=2（¹⁴/3）+1

=²⁸/3+1

= ³¹/3

=10 ⅓

谢谢

Comments

你计算三角形忘记除2了，除2了最终答案可以算出x= 4 2/3

---

谢谢版主的提点