这是五边形和四边形形成多边形的图案:
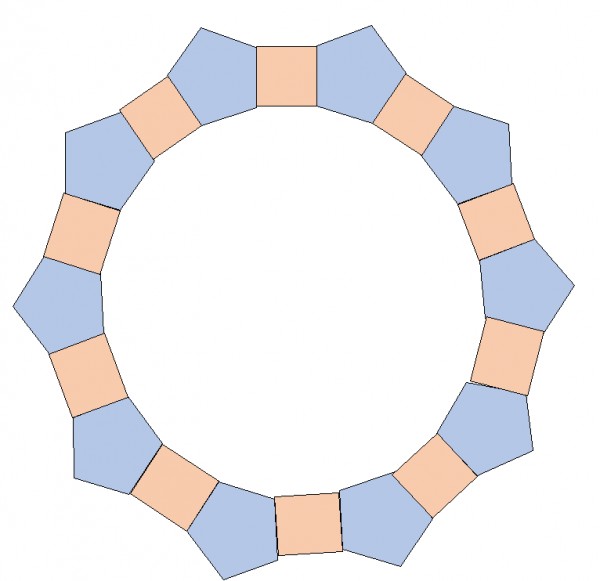
多边形有3种公式:
【1】Total sum of interior angles 内角的总和:
(n-2)x180º
.
【2】Interior angles 单个内角:
(n-2)x180º / n
.
【3】Exterior angle 外角:
360º/ n
第一步找出四边形和五边形的内角,然后加起来
第二步找出四边形和五边形的外角
第三步找出多边形的外角
第四步找出多边形边的数量
第五步找出四边形和五边形的数量
第一步
找出四边形和五边形的内角,然后加起来
公式【2】Interior angles 单个内角:
(n-2)x180º / n
.
四边形内角:
(n-2) x 180º = (4-2) x 180º
= 90º
.
五边形内角:
(n-2) x 180º = (5-2) x 180º
=108º
.
总共内角:
90º + 108º = 198º
注:四边形和五边形的总内角是形成多边形的外角
第二步
找出四边形和五边形的外角
360º - 198º = 162°
注:四边形和五边形的外角是形成多边形的内角
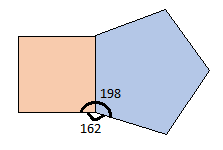
四边形和五边形的单个内角总数
第三步
找出多边形的外角,为了找出多边形边的数量
180º - 162° = 18º
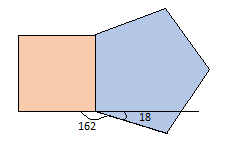
第四步
找出多边形边的数量
公式【3】Exterior angle 外角:
360º/ n
.
18º = 360º / n
n = 360º / 18º
n = 20
知道了多边形有20边
第五步
找出四边形和五边形的数量
四边形和五边形都是用底部形成多边形意思是四边形和五边形都是各种用一边来形成多边形。如图:
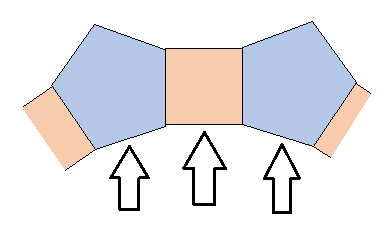
所以四边形和五边形各种用一边,所以除2就能找到四边形和五边形各自的数量:
20 / 2 = 10
四边形和五边形各自用了10个来形成多边形 (20边形)
以上是我自己的算法