其实不是第一张没有减的符号只要有第二张有,而是因为那个减的符号隐藏在了算式的里面,只是第二张没有做算式就直接把数字拉了出来。这边我们可以把第二张的题目也拿去放进算式就能知道真相了。
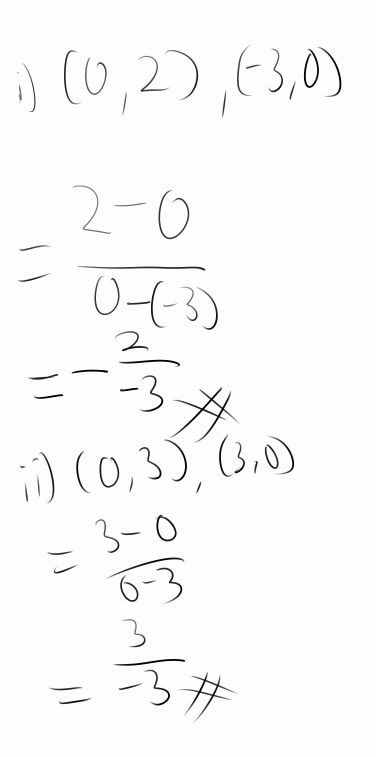 (字太丑不要介意,因为我没有用画板做数学过。。。)
(字太丑不要介意,因为我没有用画板做数学过。。。)
这边可以可以很明显的看到即使我没有特地去加减符号,但是经过了演算那个减还是会自己跑出来。所以证明了减符号其实是为了方便直接跳过算式而给答案加上的。可是个方法只能用在当x和y都分别落在自己的intercept上,就比如这题。因为在intercept上只有一个有效数字(一个数和一个零),也就是说你不用算答案就出来了,因为数字减加零它的值都不会变。而如果坐标有两个数字的时候就一定要同过formula来得出它的答案。
之所以为什么要加减符号是因为当一条斜线的两个点都是在intercept时,一定是其中一个是x而另一个是y。这个情况就使到有一定有其中一个是减掉零而另一个是被零减(你可以找几个坐标在intercept的题目来实验一下,你会发现这个是定了的)。重点来了,数字减零不会有任何变化,而被零减的那个就有问题了。因为任何数字被零减都会变成负数化,而正负得负,负负得正,所以其实就是被零减的数字会带减符号,所以凡是跳过算式的斜度都要加一个减符号。
正数的斜度和负数的斜度其实差别不大。只是正数的是朝向右上角而负数的是朝向左上角。(你看你的课本一个会有一个苦脸,然后在它的眉毛上些一个加和在另一个加上一个减。我当时看到时觉得很搞笑 ,你可以去找找看,我忘记是第几页了。)
,你可以去找找看,我忘记是第几页了。)
重写:
斜度的formula是y1-y2/x1-x2。但是在两个点坐标都落在,intercept时我们就可以用一个特别的formula那就是-y intercept/x intercept,这种情况下才需要在formula前加上减的符号。你去看你放的example会发现第二张的点都是落在paksi上的。而第一张不可以用这个formula的原因是因为它的点都不是落在intercept上。怎么知道坐标的点是不是落在intercept呢?落在intercept的坐标都会有一个特点,那就是either它的x是0或者是它的y是0。你去观察那些在intercept的点,它们坐标的x和y一定会有其中一个是0。
为什么只有在intercept的点才可以用这个formula呢?这个就比较比较难解释了,所以要看几个examples。这里有几个题目,
1.)(0,2),(4,0) + +
2.)(0,-5),(1,0) - +
3.)(0,3),(-2,0) + -
4.)(0,-4),(-1,0) - -
为了确保准确性,我准备了几个不同的负正的题目。
1.)=2-0/0-4
=2/-4
2.)=-5-0/0-1
=-5/-1
=5/1
3.)=3-0/0-(-2)
=3/2
4.)=-4-0/0-(-1)
=-4/1
你有发现吗?即使我不加上减符号,出来的答案却都和加了减算出来的答案一样。如果你有仔细观察我写的方程式,你会发现前半段减零的基本没变化,因为任何数字减零都是拿回原本的数字。而问题就出在后半段,零减别的数字却有让数字加上减的效果。所以那些为了方便不算算式的人就发明了这个formula-y intercept/x intercept。因为其实intercept在formula里面基本没变化只是加了一个减,所以它们就用这个捷径造了一个新的formula,但是这个formula只对在intercept上的点有效。(而外:两个点都在intercept的一定可以用这个formula但只有一个点在intercept的话就要看你y1-y2还是y2-y1,你不是很需要知道所以我没有写,可是你想知道的话我可以另外写。)
如果还有什么不明白的可以尽量问!•ᴗ•