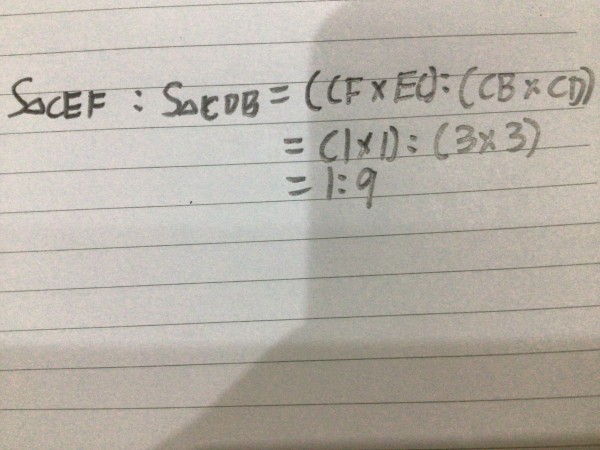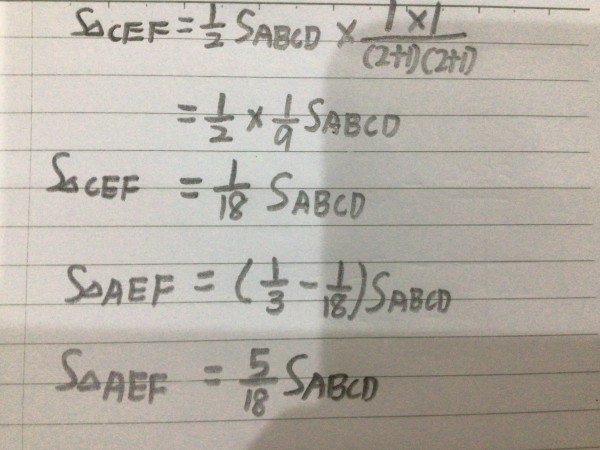注意: 我会用 “S” 来表示什么什么图形的面积。
概念:
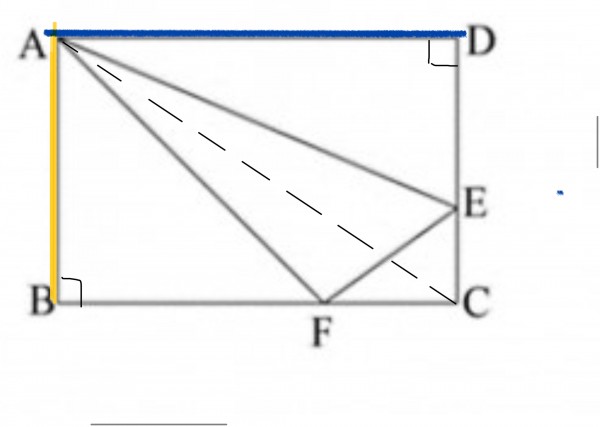
连接 AC。
三角形 ADE 和 AEC 都有公共的高 ,AD。所以他们 是等 高三角形。
同理,三角形 ABF 和 三角形也有公共的高,AB。所以他们是等高三角形。
【有些人可能不明白我说的话。三角形 ADE 的面积 1/2 ✖️ AD ✖️DE ,三角形 AEC 的面积 1/2 ✖️AD ✖️ EC。所以这两个三角形在计算面积时 有公共的高。】
定理: 如果他们的高 相等,这些三角形的面积之比 是 该三角形 底边 长度 的比。
可以看下图: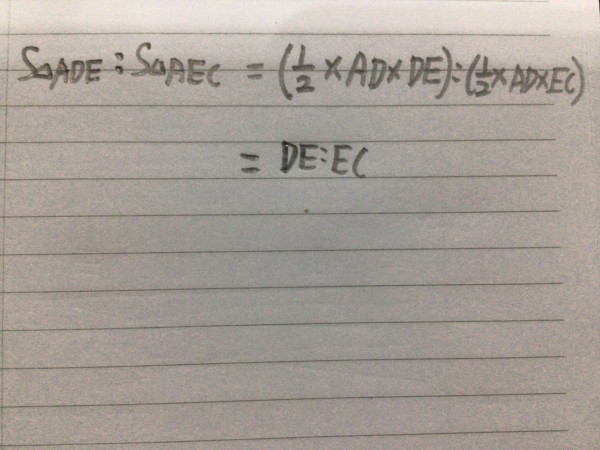
开始解答这道题:
步骤一: 设 长方形 ABCD 面积为 x,连接 AC。【继续看下图】
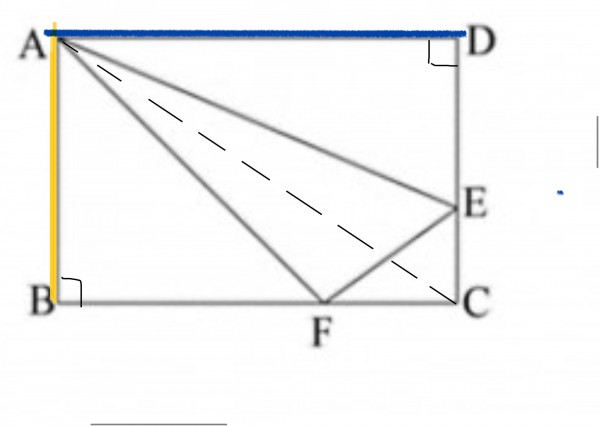
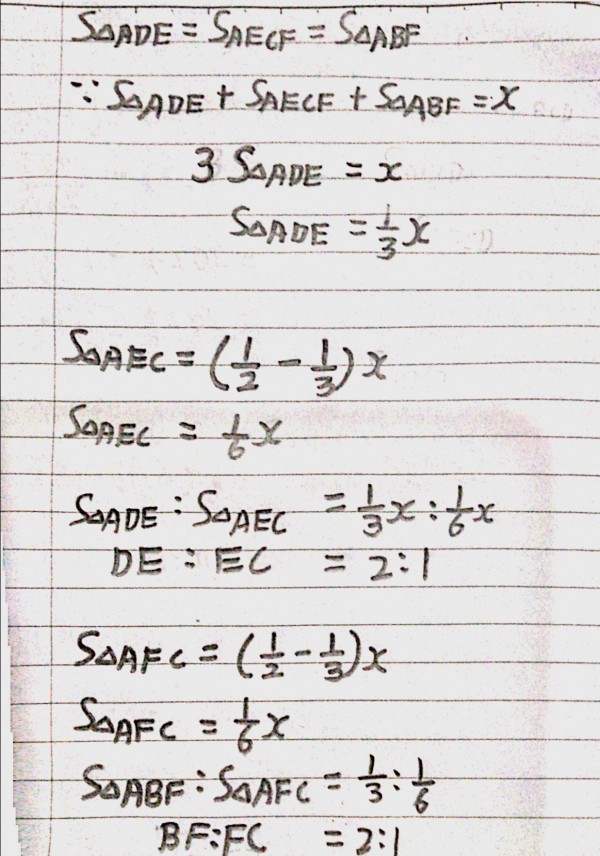
步骤二:连接 BD,如果你会 鸟头模型 的话,这一题就轻易而解。如果你不会,就要连接 BE 或 DF。(连接那一条线都一样可以算出答案)。
如果我使用鸟头模型,算式如下: