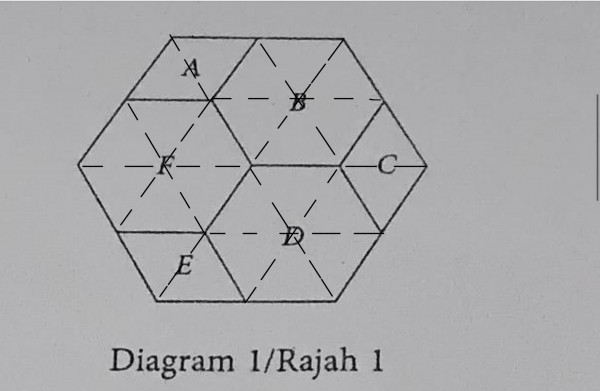
现在,这个大个的 正六边形分成 24 个 相同大小的 equilateral triangle ,所以 这24 个 equilateral triangle 的面积相同。
region C 现在被分成 2个 相等的 equilateral triangle。
Probability that the dart hits region C
= 2 / (5+7+7+5)
=2 / 24
=1/12
补充:(不用写 working) 为什么 这里的全部 等边三角形 的 大小和面积相等?
概念1: 正六边形最长的对角线是两侧顶点的对角线 , (下图:) 的边长 是 正六边形的一半,这三条对角线将六边形 分成 6个 形状大小一样的等边三角形。
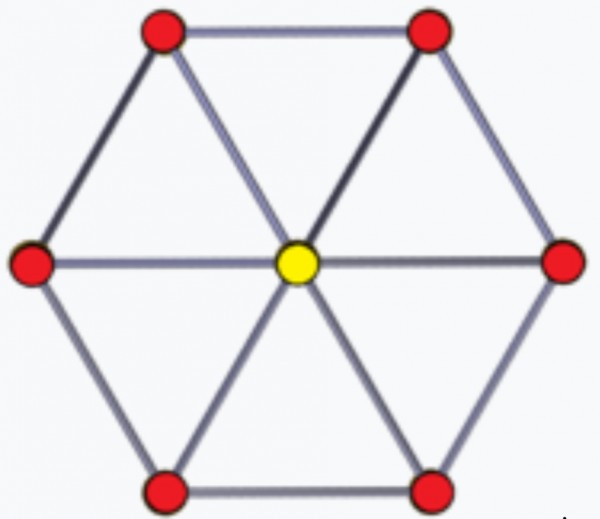
The diagonals that connect the two opposite vertices of a regular hexagon are the longest diagonal, the length of the diagonal is half of the the length of the sides of a regular hexagon. The three longest diagonals divide a regular hexagon into 6 same-sized and shaped equilateral triangles.
- 回到问题,我们先画 最大的 六边形的对角线。(正六边形的 每个内角为 120º),就这样我们可以将 region A, C, E 分别 分成 一个 等边三角形。【图1】
- 因为最大的正六边形的每个内角也为 120°,所以 可以将 region A, C, E 分别分成两个等边三角形。【图2】
- 为 region B, D, F 画上 对角线,将 正六边形分别分 成 6 个 等边三角形。
- 就这样,我们将 最大的正六边形 分成 24 个 小的 等边三角形。
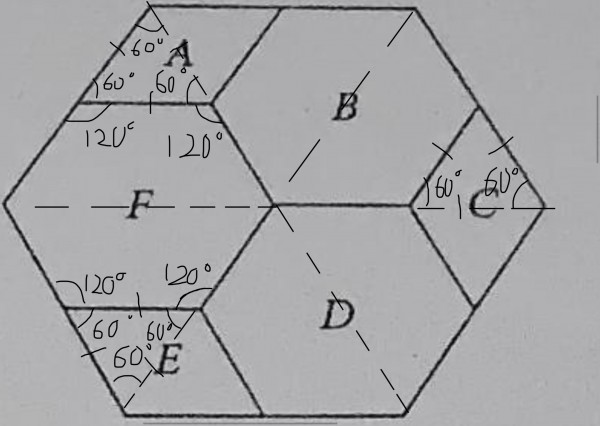
图片1
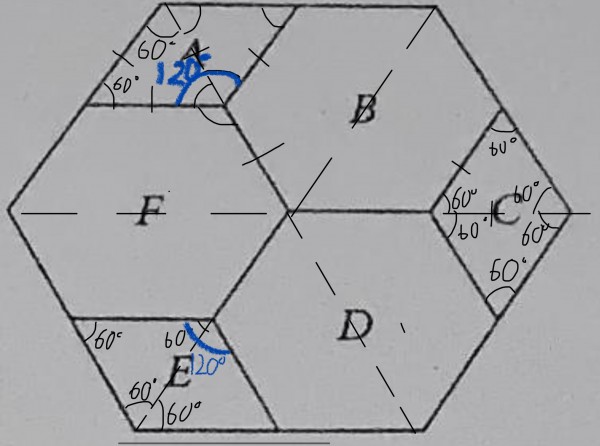
图片2